Корпоративное управление и инновационное развитие экономики Севера
Вестник Научно-исследовательского центра 
корпоративного права, управления и венчурного инвестирования
Сыктывкарского государственного университета

В соответствии с решениями президиума Высшей аттестационной комиссии Минобрнауки России с 19.02.2010 г. входит в Перечень ведущих рецензируемых научных журналов и изданий, в которых должны быть опубликованы основные научные результаты диссертаций на соискание ученых степеней кандидата и доктора наук

МОДЕЛЬ ПОСТРОЕНИЯ ОПТИМАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ШАГОВ ТРУДОВОГО ПРОЦЕССА

Гаджиев Р. И.

В статье представлена математическая модель оптимального распределения трудовых действий, построенная по методу динамического программирования. Основное внимание уделено оценкам переходов отдельных шагов трудового процесса. Описывается подход вероятностного моделирования трудового процесса сотрудника предприятия. Использование разработанной модели предполагается на предприятиях с системой мониторинга и управления трудовыми процессами сотрудников.

The mathematical model of optimal labor actions distribution, built on the dynamic programming method are stated in the article. Main focus is on transition estimates of the individual workflows elements. Described the probabilistic approach of modeling employee workflow. The usage of the described model supposed in the companies with the monitoring and management employee workflows system.

Ключевые слова: управление трудовым процессом, трудоемкость, моделирование трудового процесса, динамическое программирование, вероятностное моделирование.

Keywords: labor processes management, laboriousness, workflows modeling, dynamic programming, probabilistic modeling.

Планирование времени проекта, прогнозирование трудозатрат или любой другой анализ трудовых процессов непосредственно связан с производительностью исполнителя трудовых процессов. Однако производительность сотрудника предприятия не является величиной постоянной, её природа изменчива и имеет нелинейный характер. Очевидно, что в течение рабочего дня в силу разных обстоятельств динамика производительности сотрудника может меняться. Некоторые предприятия проводят расчеты норм труда из выборочной группы или всех сотрудников предприятия, не акцентируя внимание на то, что отдельные сотрудники отличаются друг от друга значениями индивидуальной интенсивности труда и потенциальной  продуктивностью. Эти усредненные величины лишь отчасти коррелируют с повседневной, меняющейся в течение рабочего дня, продуктивностью отдельных лиц. Именно поэтому данный метод не подходит для управления трудовыми ресурсами в режиме реального времени. Длительность трудовых действий исполнителя в период работы над единицей продукта труда имеет вариативный характер, в силу этого существует необходимость исследования трудовых процессов с позиций вероятностного подхода.

Как известно, для наиболее эффективной работы предприятия продуктивность сотрудников должна быть максимальной. Мониторинг и управление трудовым процессом сотрудника (в режиме реального времени) показывают значительное влияние на его конечную производительность, если данному управлению предшествует системный анализ результатов мониторинга [1]. Ведь, как известно, если запланированное исполнителем время для решения производственной задачи больше необходимого, то трудовой процесс «растягивается» на запланированный период, а не решается исполнителем в соответствии с реально необходимым объемом времени [2]. В обратном же случае, если время слишком короткое, это приводит к необходимости сверхурочной работы. Видимо наиболее эффективный режим находится где-то между этими двумя крайностями и прямо зависит от планируемой продолжительности работы.

Именно поэтому в вопросе управления трудовыми процессами среди факторов оказывающих влияние на конечную производительность сотрудников, стоит выделить: динамической контроль трудового процесса, использование математического аппарата при анализе и разработке рекомендаций лицам, принимающим решения, а также объективную оценку возможностей и способностей исполнителя.

Как показывает анализ результатов мониторинга трудовой деятельности работников, продуктивность отдельных шагов в трудовом процессе имеет стохастический характер [3]. Это говорит о том, что управление производительностью сотрудника предприятия непосредственно связано с анализом функции распределения как временных, так и качественных характеристик элементов трудового процесса, что имеет решающее значение в вопросе оптимального моделирования трудовых процессов.

Данные обстоятельства приводят автора к позиции вероятностного подхода в задаче моделирования распределения трудовых действий. Предлагаемая автором модель учитывает изменчивость продуктивности сотрудника в течение рабочего дня, и строит распределение согласно функциям оценок, разработанных на основе как временных, так и качественных характеристик его трудовой деятельности.

Разработка математической модели построения оптимальной последовательности шагов трудового процесса.

Моделирование трудового процесса сотрудника строится  на базе вероятностного подхода. Необходимым условием использования вероятностной модели является наличие статистической базы зарегистрированных компонентов модели и их характеристик, которые регистрируются в процессе трудовой деятельности сотрудника предприятия. Под компонентами вероятностной модели предполагаются действия сотрудника, предметы труда и их свойства.

Вероятностная модель трудового процесса сотрудника представляется следующим кортежем:

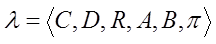,                                                                                                                (1)

где C – типы продуктов труда сотрудника предприятия. Ввиду возможности исполнения сотрудником  разнородной трудовой деятельности в данной модели каждый из типов производственных заданий характеризует конкретный тип продукта труда получаемый в результате исполнения трудового процесса сотрудником предприятия. Не только разные сотрудники, но и один и тот же человек может получить одинаковый тип продукта труда,  в результате исполнения разнородных трудовых процессов. Множество типов продуктов труда представим в виде набора C={c₁,c₂,…,c_K}, где K – количество сотрудников предприятия. Количество продуктов труда в трудовой деятельности k-го сотрудника предприятия выразим через переменную L;

D – множество трудовых действий сотрудника предприятия в ходе исполнения цели c_k. Предполагается, что действия в модели соответствуют реальным действиям, исполняемым сотрудником при решении определенной задачи. Область допустимых действий по конкретному шагу в модели определяется историей исполнений действий в данном шаге и по данному типу задания. Модель предусматривает повторы одного и того же действия над определенным предметом труда. Однако одновременное исполнение двух или более действий в модели не предусматривается. Также надо заметить, что трудовые процессы сотрудника могут характеризоваться отличием не только в структуре или последовательности исполняемых действий, но также и различием в видах используемых действий. Обозначим набор действий модели множеством D={d₁,d₂,…,d_N}, где N – количество действий в модели. Текущее действие в момент времени обозначим как t_z, где Z – это количество шагов в трудовом процессе;

R – множество всех предметов труда, обрабатываемых в ходе решения задачи c_k сотрудником предприятия. Множество наблюдаемых предметов труда представим в виде R={r₁,r₂,…,r_M}, где M – количество предметов труда в модели. В контексте данной модели предметом труда является объект, имеющий в изначальном своем виде необходимые для производства свойства или приобретший их в результате внешнего воздействия сотрудника предприятия. Представим свойства предмета труда в виде компонентов вектора r_u={x₁,x₂,…,x_S}, где S - количество свойств предмета труда r_u.

Очевидно также, что условием разработки определенного типа продукта труда является обработка (до необходимых свойств) всех предметов труда, входящих в его множество. Отметим и то, что обработка предмета труда сотрудником предприятия в момент времени 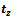 может происходить лишь с одним предметом труда.

 Выразим через 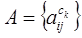  матрицу вероятностей переходов, где

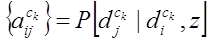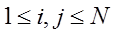,                                                                                         (2)

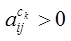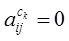Вероятность того, что сотрудник k исполнивший действие d_i на шаге z, начнет выполнять действие d_j на шаге z+1, в ходе работы над типом продукта c. В случае если для всяких двух действий в модели возможен переход из одного действия в другое, то для любых i,j вероятность перехода  . В других случаях  для некоторых i,j.

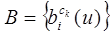 – распределение вероятностей работы с предметами труда при исполнении i-го действия, где

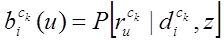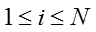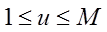, , ,                                                                     (3)

то есть вероятность того, что сотрудник, в момент времени t_z выполняющий действие d_i работает с предметом труда r_u.

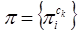, – распределение вероятностей первоначального действия, где

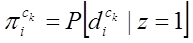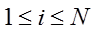, ,                                                                                             (4)

вероятность того, что d_i  - начальное действие для сотрудника k при работе над продуктом труда c.

Таким образом, прогнозируемую последовательность трудового процесса сотрудника k  по продукту 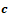 представим как:

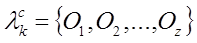, где                                                                                                 (5)

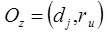– прогнозируемое действие и предмет труда на шаге z.

Как известно, для некоторых индивидов существуют фазы в трудовом процессе, производительность которых может быть низкой в соотношении с предыдущими исполнениями, однако в конечном счете общая производительность данного исполнения может оказаться выше. Исходя из этого утверждения, автор строит модель, в которой распределение трудовых действий приводит к наиболее высокой общей производительности. Задачу можно представить как задачу динамического программирования с конечным числом этапов. Под этапами подразумеваются шаги в трудовом процессе сотрудника. Очевидно, что наиболее оптимальным распределением трудовых действий будет то, которое приведет к наибольшей ожидаемой производительности через Z шагов. Ожидаемую общую производительность представим как функцию «оценки». Тогда задача будет состоять в таком распределении шагов, которое максимизировало бы математическое ожидание функции оценки в Z-шаговом процессе.

Выразим через f_z(i) функцию оценки, то есть математическое ожидание, полученное на шагах от z до Z при условии, что исполнитель совершает тип действия i на шаге z. Уравнение функции оценки сотрудника k по цели c является обратно рекуррентным и выглядит так:

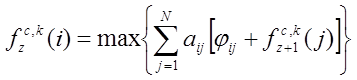, z=1,2,…, Z                                                                (6)

,

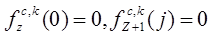где a_ij – значение из матрицы вероятностей переходов модели (1) и определяется согласно (2).

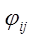– это единичная оценка, которую получит сотрудник при переходе из типа действия i в j. То есть данная переменная выражает коротковременную оценку производительности, которую исполнит сотрудник в данном переходе.

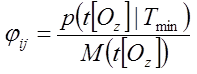,                                                                                                           (7)

где M(t[O_z]) – математическое ожидание длительности действия в шаге O_z.

p(t[O_z]|T_min) – условная вероятность появления значения времени t[O_z] при минимальной общей трудоемкости T_min трудового процесса сотрудника k по продукту труда c Данная вероятность рассчитывается как

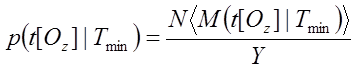,                                                                                 (8)

где 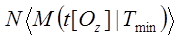 – количество повторений определенной длительности действия пары O_z, равное математическому ожиданию зафиксированных значений времени при минимальной общей трудоемкости.

Y – общее количество зафиксированных значений времени по паре O_z.

Уравнение (6) построено на основании того, что нарастающая оценка производительности 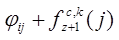 становится  в результате переходов из действия d_i на шаге z в действие d_j на шаге z+1 с вероятностью a_ij. Просчитав суммарную оценку для переходов по всем трудовым действиям, можно предположить, что сотрудник выберет то действие, которое приводит к максимальной суммарной оценке. Финальный вид модели можно представить следующим образом:

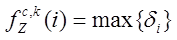
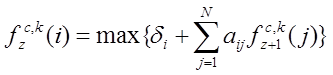, z=1,2,…, Z-1,                                                                 (9)

где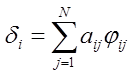                                                                                                                             

Приведем пример работы модели (9). Пусть имеются 3 типа действий в модели. Значения матрицы переходных вероятностей представим следующим образом:

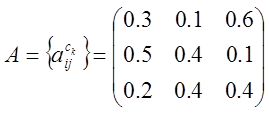
Значения оценок для каждого перехода также представим в виде матрицы:

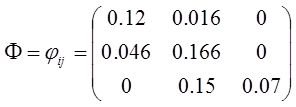
В этом случае значения 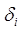 будут равны:

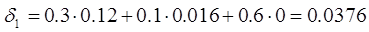
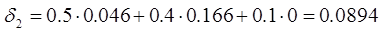
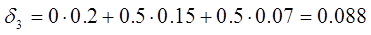
Таким образом, если на начальном шаге исполнитель совершает первый тип действия, то при переходе на следующий шаг суммарный коэффициент оценки производительности составит 0.0376. В случае перехода со второго типа действия суммарная оценка составит 0.0894, а для третьего типа - 0.088. Соответственно, оптимальным решением в данном случае будет выбор второго типа действия. Продлим пример еще на два шага. Для следующего шага функция оценки примет вид:

.

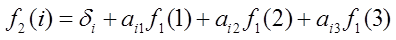Посчитаем эти значения для каждого типа действия:

.

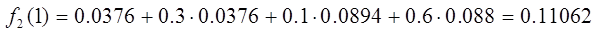
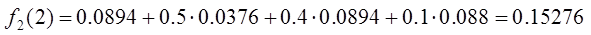
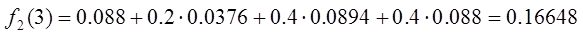И последний шаг примет значения:

.

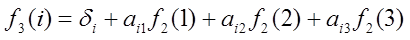
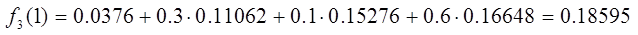
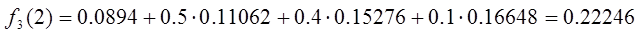
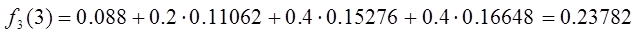Из полученных данных можно сделать вывод, что оптимальным решением на первом и втором шаге трудового процесса является выбор третьего типа действия. А на третьем шаге исполнителю стоит выбрать второй тип действия. Именно такое распределение трудовых действий приводит к наиболее продуктивному по прогнозу, трудовому процессу сотрудника предприятия.

Проверка модели.

Для проверки достоверности разработанной модели проведено статистическое исследование: в период с 01.06.2012 по 29.06.2012 исследование проводилось на трудовых процессах сотрудников «Отдела обработки изображений» компании «Апликот», а именно на монтажерах. В период исследования каждый из 20-ти монтажеров следовал рекомендациям модели (6), которые выводились на дисплее его настольного компьютера. График работы монтажеров был сменный – 2 рабочих дня через 2 выходных. В течение рабочего дня каждый из монтажеров исполнял минимум 120 однотипных трудовых процессов по обработке изображений, и именно такое количество использовалось в исследовании. Информационной системой регистрировалась длительность каждого трудового процесса и значение модели (6) по данному трудовому процессу. Также фиксация значений происходила по каждому монтажеру и каждый день в период исследования. 

Из зафиксированных данных по каждому дню и по каждому отдельному монтажеру, определялся коэффициент корреляции Пирсона R_k данных длительности отдельного трудового процесса и значения рассчитанной модели (6) для данного трудового процесса. Результаты расчёта для отдельного монтажера на первый день исследования представлены в таблице 1.

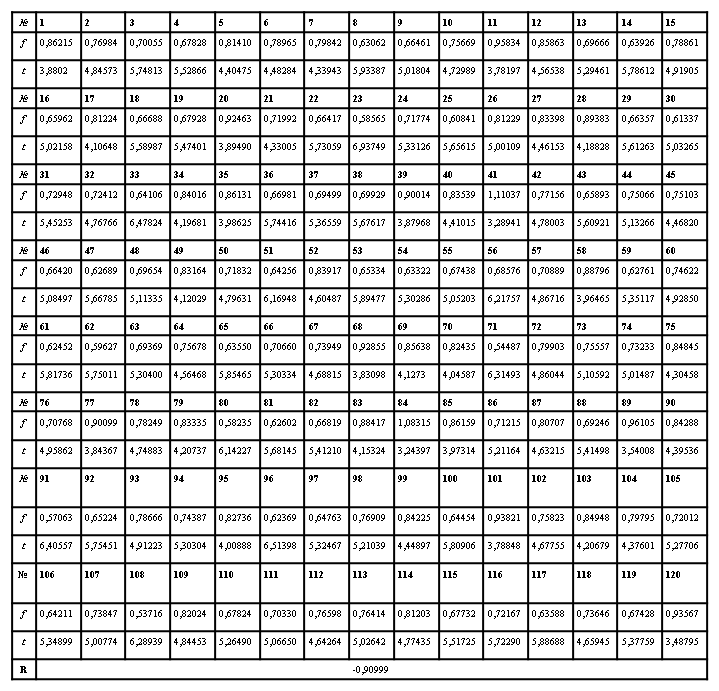
Таблица 1.

Результаты измерения длительности трудовых процессов t (в мин.) и значения модели f (6) по отдельному монтажеру на 01.06.2012.

На основе полученных результатов определялись данные для проведения итогового регрессионного анализа. Данные для анализа отбирались каждый день на протяжении периода с 01.06.2012 по 29.06.2012. В конце каждого рабочего дня из расчётов по всем монтажерам определялось минимальное значение коэффициента корреляции Пирсона R_kàmin, при R_k>0,232  (для вероятности ошибки 0,1). После чего из выбранной таблицы рассчитывалось среднее значение длительности трудового процесса t 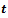 и соответствующее ей значение модели f (6) и вносилось в таблицу по данному рабочему дню. Конечная таблица для итогового регрессионного анализа представлена в таблице 2.

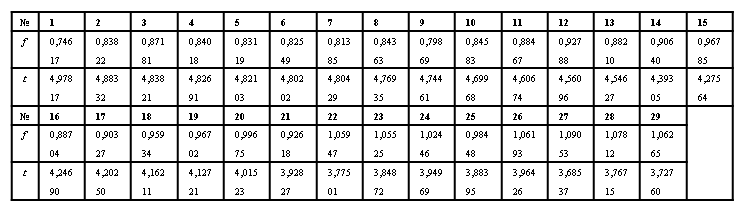
Таблица 2.

Экспериментальные данные для проверки достоверности модели (6).

Для проверки достоверности модели (6) автором был проведен регрессионный анализ зависимости переменной 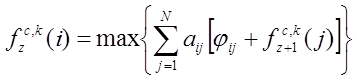 от t. Согласно исследованию, эта зависимость должна быть обратно пропорциональной: f=a-bt.

Для полученного динамического ряда с помощью метода наименьших квадратов был определен линейный тренд: f=1,8507-0,2129t (рис. 1). На рис. 1 можно увидеть, что при постепенном уменьшении длительности трудового процесса увеличиваются значения модели (6), которая определяет оптимальную последовательность трудовых действий для общей трудоемкости отдельного трудового процесса.

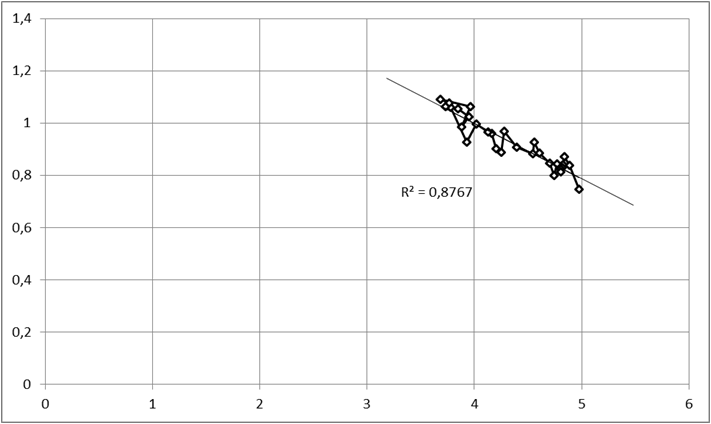
Рис. 2. Аппроксимация значений 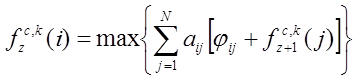 по каждому дню в период с 01.06.2012 по 29.06.2012.

Из значения величины достоверности аппроксимации R²=0,8767 можно сделать вывод о явной близости модели и эмпирических данных. Из чего следует, что полученное значение коэффициента детерминации (R²=0,8767) свидетельствует о достоверности разработанной модели (6) для выборочной совокупности исследования (объемом в 30 случаев).

Таким образом, автором разработана и описана модель, позволяющая определить последовательность трудовых действий, которая наиболее всего минимизирует суммарные ожидаемые издержки от трудовой деятельности сотрудника. Данная модель может быть использована в качестве конкретного научного обеспечения при разработке систем поддержки принятия решений и управления трудовыми процессами.

 
Список литературы:

1. Рудик Е. В. Мониторинг производительности труда на промышленном предприятии и в вертикально-интегрированной структуре: дис. канд. экон. наук: 08.00.05. – Краснодар, 2010.
2. Barseghyan L., DiCecio R. Finite Endogenous productivity and multiple steady states. // Federal reserve bank of St. Louis, 2008.
3. Миускова Р. П., Киреева Л. Е., К вопросу разработки и обновления нормативов времени индексным методом / Труд и норма. – 2012. – №1. – С. 24-30.
4. Френкель А. А. Прогнозирование производительности труда: методы и модели. — М.: Экономика, 1989.
5. Боровков А. А. Математическая статистика. — М.: Наука, 1984.
6. Беллман Р. Динамическое программирование. — М.: Изд-во иностранной литературы, 1960.

 
Literature:

1. Rudik E.V. Productivity monitoring in industry and in the vertically integrated structure: dis. of the econ. sc.: 08.00.05. - Krasnodar, 2010.
2. Barseghyan L., DiCecio R. Finite Endogenous productivity and multiple steady states. // Federal reserve bank of St. Louis, 2008.
3. Miuskova R.P., Kireeva L. E., About development and update of the time index method / Trud i norma. – 2012. – №1. – P. 24-30.
4. Frenkel A. A. Forecasting productivity: Methods and Models. — M.: Ekonomika, 1989.
5. Borovkov A. A. Mathematical statistics. — M.: Nauka, 1984.
6. Bellman R. Dynamic Programming. // M.: Izdatelstvo inostrannoy literatury, 1960.