|
|
оценка
эффективности вариантов развития
региональных энергосистем с учетом надежности электроснабжения
потребителей:
теоретический аспект
Чукреев Ю.Я.
В статье рассмотрены возможности опосредованного учета фактора надежности в задаче оценки эффективности вариантов развития региональных энергосистем, работающих в составе Единой электроэнергетической системы страны для условий реструктуризации электроэнергетической отрасли. Особое внимание уделено теоретическому обоснованию индексов нормирования надежности соответствующих минимуму приведенных затрат в создании резервов мощности территориальных (региональных) энергосистем и запасов пропускных способностей связей, их соединяющих
This paper presents different approaches of indirect reliability assessment in alternative versions of evolution analysis for regional power systems issue. Regional power systems considered as part of United Russian power system with conversion conditions assumed. Theoretical positions of indices of power system adequacy approval have been taken into consideration. In paper have been studied reliability indices which are equivalent to minimal costs for generation reserve and capacity of lines reserve
Ключевые слова: электроэнергетическая система, территориальная зона, приведенные затраты, показатели надежности, затраты, резерв мощности, пропускная способность связи
Keywords: power system, area, costs, reliability indices, power reserve, line capacity
При
разработке и обосновании перспективных балансов
мощности электроэнергетических систем (региональных, объединенных и ЕЭС
России
в целом) в условиях централизованного управления отраслью существовала
эффективная иерархическая система. Она включала в себя множество стадий
как территориального,
так и временного уровней иерархии, причем на каждой из них происходило
уточнение решения предыдущих стадий. В ее рамках разрабатывалась
стратегия
развития региональных энергосистем на перспективу от 20 до 30 лет и
планы
развития генерирующих источников и линий электропередачи на
среднесрочный (5-10
лет) и краткосрочный периоды (3-5 лет), обеспечивающие
оптимальное сочетание капитальных вложений, эксплуатационных затрат и
ущербов
от ненадежности электроснабжения потребителей [1]. При этом обеспечение
надежности стояло на одном из первых мест среди основных критериев
принятия
решений при управлении развитием ЭЭС [2, 3].
В
условиях либерализации отношений в процесс анализа
и принятия решений по развитию региональной электроэнергетики
оказываются
вовлеченными многие участники (субъекты отношений) с несовпадающими
интересами:
электроэнергетические компании (генерирующие, сетевые и сбытовые),
потребители,
инвесторы, общественные организации, федеральные и региональные органы
власти.
По сути, методология обоснования развития электроэнергетических систем
(ЭЭС)
сегодня претерпела определенную трансформацию от централизованного
государственного планирования к новой парадигме многостороннего
процесса
обоснования решений и создания механизмов их реализации в условиях
неопределенности,
многокритериальности и множественности интересов
[4, 5, 6].
Развитие
генерирующих источников (создание
резервов мощности) и строительство линий электропередачи для повышения
запасов пропускной
способности системообразующих связей являются мероприятиями весьма
дорогостоящими.
Поэтому они должны тщательно обосновываться и быть выгодными для
потенциальных
инвесторов. Обоснование этих мероприятий независимо от принятых
принципов
управления отраслью должно базироваться на минимизации функционала
приведенных
или дисконтных затрат [1]. Приведенные к одному году (Тр = 8760 ч)
затраты 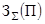 в зависимости от
средств обеспечения
надежности (П) включают в себя затраты на поддержание резервов
генерирующей мощности
(Rj)
в зависимости от
средств обеспечения
надежности (П) включают в себя затраты на поддержание резервов
генерирующей мощности
(Rj)
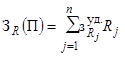 ,
пропускной способности (
,
пропускной способности (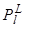 )
l -х
связей
)
l -х
связей 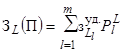 (для концентрированной
ЭЭС равны нулю ;
(для концентрированной
ЭЭС равны нулю ; 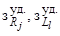 – удельные
затраты (руб./кВт) соответственно на создание
резерва генерирующей мощности в j -й
территориальной зоне ЭЭС и в усиление связей) и так
называемые компенсационные затраты
– удельные
затраты (руб./кВт) соответственно на создание
резерва генерирующей мощности в j -й
территориальной зоне ЭЭС и в усиление связей) и так
называемые компенсационные затраты 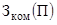 от
ненадежности электроснабжения потребителей,
т.е.
от
ненадежности электроснабжения потребителей,
т.е.
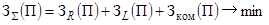 .
(1)
.
(1)
Получение
численных значений первых
двух слагаемых выражения (1) как в условиях централизованного
управления
электроэнергетической отрасли, так и в условиях рыночных отношений
сложностей
не вызывает. Получение третьего требует оценки количественных
показателей
надежности рассматриваемых вариантов развития ЭЭС в виде
математического
ожидания ущерба от ненадежности электроснабжения потребителей. Задача
крайне
сложная, требующая определенной информационной основы, модельного
обеспечения и
значительных затрат времени счета на вычислительных средствах.
Достаточно
слабый на сегодняшний день уровень информационной обеспеченности по
стоимостным
показателям ущербов от ненадежности электроснабжения дает основания
использовать накопленный для условий централизованного управления
отраслью опыт
учета компенсационных затрат от ненадежности и опосредованно применить
его для
условий реформирования электроэнергетики страны. Именно теоретические
положения
этой проблемы раскрываются в статье применительно к схемам развития
ЭЭС.
Оптимальному
уровню надежности в концентрированной ЭЭС соответствует выражение
минимума
приведенных затрат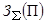 (1)
без включения в него сетевой составляющей (второго слагаемого). При
долгосрочном планировании развития ЭЭС можно принять допущения о
линейной
взаимосвязи затрат на создание резерва генерирующей мощности
(1)
без включения в него сетевой составляющей (второго слагаемого). При
долгосрочном планировании развития ЭЭС можно принять допущения о
линейной
взаимосвязи затрат на создание резерва генерирующей мощности 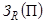 с самой величиной
резерва
с самой величиной
резерва 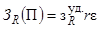 (
(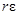 – величина
резерва мощности,
выраженная через наименьший по мощности агрегат
– величина
резерва мощности,
выраженная через наименьший по мощности агрегат 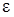 и их число
и их число 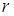 )
и о пропорциональности математического ожидания
компенсационных затрат
)
и о пропорциональности математического ожидания
компенсационных затрат 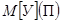 энергии,
недопоставленной потребителям
энергии,
недопоставленной потребителям 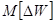 ,
т.е.
,
т.е. 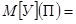
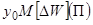 .
При таких допущениях можно легко определить условия
минимума функционала (1)
.
При таких допущениях можно легко определить условия
минимума функционала (1)
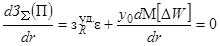 .
(2)
.
(2)
В
работе [7] для концентрированной ЭЭС показана строгая
связь интегральной вероятности появления дефицита мощности с
показателем 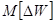 :
:
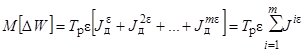 ,
(3)
,
(3)
где
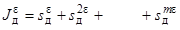 ;
;
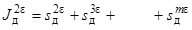 – интегральные
вероятности появления дефицита мощности
в ε и более, в 2ε и более МВт и т.д.
соответственно.
– интегральные
вероятности появления дефицита мощности
в ε и более, в 2ε и более МВт и т.д.
соответственно.
При
увеличении резерва мощности R
в ЭЭС на величину ε МВт величина
математического ожидания недоотпуска электроэнергии в соответствии с
выражением
(3) уменьшится и составит:
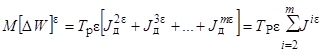 . (4)
. (4)
Отличие
(3) и (4) как раз и определит производную  :
:
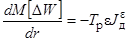 .
(5)
.
(5)
Таким
образом, для концентрированной энергосистемы показатель балансовой
надежности в
виде ![]() пропорционален
производной от математического ожидания недоотпуска электроэнергии по
резерву
генерирующей мощности R.
Это позволяет использовать его
для целей нормирования. С учетом (5) выражение (2) может быть
представлено в
широко известной форме:
пропорционален
производной от математического ожидания недоотпуска электроэнергии по
резерву
генерирующей мощности R.
Это позволяет использовать его
для целей нормирования. С учетом (5) выражение (2) может быть
представлено в
широко известной форме:
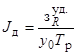 .
(6)
.
(6)
Несмотря
на то, что интегральная вероятность
появления дефицита мощности (Jд)
непосредственно не связана с величиной компенсационных затрат от
ненадежности,
она тем не менее соответствует минимуму приведенных затрат (1).
Для
многозонной ЭЭС условием оптимальности резервов генерирующей мощности
отдельных
территориальных зон –
региональных энергосистем, и запасов пропускной
способности связей между ними также является минимум функционала
приведенных
затрат (1). Условием оптимальности, как и для концентрированной ЭЭС,
будет
равенство нулю частных производных от функционала приведенных затрат по
резервам мощности территориальных зон и запасам пропускной способности
связей
между ними, т.е.:
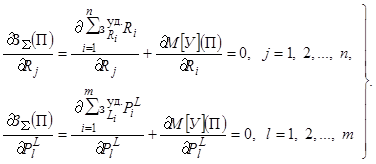 (7)
(7)
Сложность
решения системы уравнений (7) связана с
трудностями получения частных производных от компенсационных затрат
(математического ожидания ущерба потребителям) от ненадежности
электроснабжения. Искомые частные производные для многозонной ЭЭС можно
определить, применяя математический аппарат теории линейного
программирования (ЛП)
[8].
Использование
теории двойственности ЛП позволяет при
однократном решении задачи оценки показателей надежности найти такие
важные
характеристики, как вероятности появления дефицита генерирующих
мощностей в
отдельных территориальных зонах ЭЭС и вероятности превышения перетоков
мощности
запасов пропускной способности связей. В отличие от традиционного
использования
двойственных оценок для систем с детерминированным режимом
функционирования
ниже развивается подход для систем со стохастически определенным
режимом
функционирования [9]. Применение такого подхода требует определения
двойственных оценок по всему множеству моделируемых расчетных состояний
системы,
вызванных плановыми и внеплановыми выводами генерирующего и сетевого
оборудования
в ремонты.
Процесс
определения показателей балансовой
надежности в крупной ЭЭС, состоящей из множества региональных
энергосистем, состоит
из трех взаимосвязанных этапов. На первом этапе производится
моделирование
случайных k-х
состояний ЭЭС по генерации, вызванных
ненадежностью генерирующего оборудования, по нагрузке, вызванной ее
колебаниями
и ошибками прогнозирования, и по пропускной способности связей,
зависящей от
состояния режима сети и от аварийности линий электропередачи.
Особенности этого
этапа в контексте данной статьи не представляют интереса.
На
втором этапе производится оценка сформированных на первом этапе
случайных состояний
с позиций возможности обеспечения потребителей. Оценка каждого
случайного состояния
связана с решением задачи минимизации дефицита мощности в ЭЭС [10]:
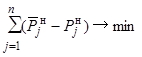 ,
(8)
,
(8)
при
ограничениях:
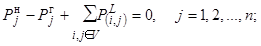 (9)
(9)
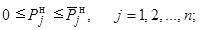 (10)
(10)
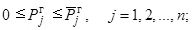 (11)
(11)
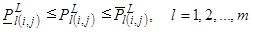 ,
(12)
,
(12)
где
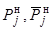 – соответственно
покрытая потребность и мощность спроса нагрузки j -й территориальной
зоны;
– соответственно
покрытая потребность и мощность спроса нагрузки j -й территориальной
зоны; 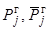 – используемая
и имеющаяся генерирующие мощности
j –й
территориальной
зоны;
– используемая
и имеющаяся генерирующие мощности
j –й
территориальной
зоны; 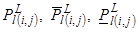 – переток
мощности по l -ой связи и его
возможные предельные значения в прямом
(из зоны i в зону j)
и обратном (из зоны j в зону i) направлениях (в
дальнейшем индексы i и j у связей будут опущены); V – множество
пар территориальных зон i и j расчетной схемы ЭЭС, имеющих между
собой связи; n(m)
–
число
территориальных зон (связей) ЭЭС.
– переток
мощности по l -ой связи и его
возможные предельные значения в прямом
(из зоны i в зону j)
и обратном (из зоны j в зону i) направлениях (в
дальнейшем индексы i и j у связей будут опущены); V – множество
пар территориальных зон i и j расчетной схемы ЭЭС, имеющих между
собой связи; n(m)
–
число
территориальных зон (связей) ЭЭС.
Формируемые
случайные состояния могут быть дефицитными
или избыточными с точки зрения рассмотрения всей ЭЭС, а не отдельных ее
территориальных
зон.
Третий
этап состоит в определении показателей надежности. Интегральная
вероятность появления
дефицита мощности в ЭЭС для периода времени 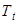 определяется суммой
вероятностей k -х состояний
системы,
в которых был дефицит генерирующей мощности. Математическое ожидание
недоотпуска электроэнергии определяется суммированием дефицитов
мощности,
взвешенных по вероятности существования всех k
-х состояний, т.е.
определяется суммой
вероятностей k -х состояний
системы,
в которых был дефицит генерирующей мощности. Математическое ожидание
недоотпуска электроэнергии определяется суммированием дефицитов
мощности,
взвешенных по вероятности существования всех k
-х состояний, т.е.
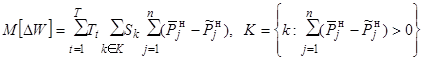 ,
(13)
,
(13)
где
K – множество
моделируемых состояний ЭЭС; 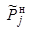 – обеспеченный
спрос нагрузки j-й территориальной зоны,
полученный в результате
решения задачи (8) при ограничениях (9)-(12).
– обеспеченный
спрос нагрузки j-й территориальной зоны,
полученный в результате
решения задачи (8) при ограничениях (9)-(12).
Математическое
ожидание недоотпуска электроэнергии связано с энергией, фактически
доставленной
потребителям (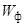 ),
выражением
),
выражением
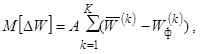 (14)
(14)
где
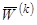 – энергия,
получаемая потребителями расчетной схемы при
– энергия,
получаемая потребителями расчетной схемы при 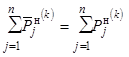 ,
т.е. при
,
т.е. при 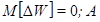 – некоторая
константа, зависящая от интервала
расчетного периода времени [9].
– некоторая
константа, зависящая от интервала
расчетного периода времени [9].
В
соответствии с теорией двойственности линейного программирования для k-го расчетного состояния системы можно
с учетом (8) и (13) записать выражение для фактически доставленной
энергии
потребителям:
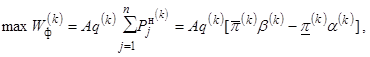 (15)
(15)
где
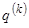 – вероятность
существования k-го расчетного
состояния;
– вероятность
существования k-го расчетного
состояния; 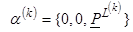 ,
,
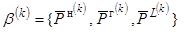 – соответственно
векторы
верхних и нижних границ изменения нагрузки
– соответственно
векторы
верхних и нижних границ изменения нагрузки 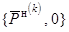 и генерирующей
мощности
и генерирующей
мощности 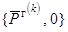 территориальных зон (10),
(11) и пропускных способностей связей
территориальных зон (10),
(11) и пропускных способностей связей 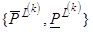 (12);
(12); 
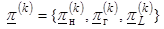 – векторы
двойственных оценок, соответствующих
границам изменения векторов верхних
– векторы
двойственных оценок, соответствующих
границам изменения векторов верхних 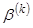 и нижних
и нижних 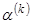 ограничений параметров
системы.
ограничений параметров
системы.
Показатель
надежности 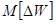 обладает свойством
аддитивности, т.е.
обладает свойством
аддитивности, т.е. 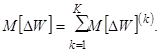 Очевидно, что этим же
свойством обладает и значение фактически доставленной потребителям электроэнергии. Поэтому
справедливо выражение
Очевидно, что этим же
свойством обладает и значение фактически доставленной потребителям электроэнергии. Поэтому
справедливо выражение
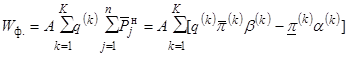 .
(16)
.
(16)
Изменение
пределов параметров системы 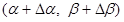 возможно только у
генерирующих мощностей территориальных зон и пропускных способностей
связей
между ними. Такое изменение приведет к следующему:
возможно только у
генерирующих мощностей территориальных зон и пропускных способностей
связей
между ними. Такое изменение приведет к следующему:
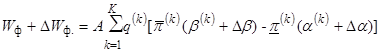 . (17)
. (17)
Равенство
(17) справедливо в рамках неизмененного
базиса [8], т.е. при сравнительно небольших значениях 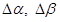 .
.
Вариация параметров 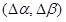 постоянна для всей
совокупности k-х расчетных
состояний.
В этих условиях изменение фактически доставленной энергии
постоянна для всей
совокупности k-х расчетных
состояний.
В этих условиях изменение фактически доставленной энергии 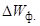 определяет и изменение
показателя надежности
определяет и изменение
показателя надежности 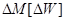 ,
т.е.
,
т.е.
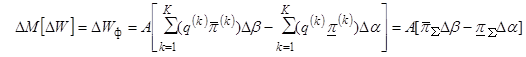 ,
(18)
,
(18)
где
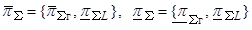 – векторы
суммарных, взвешенных по вероятности
двойственных переменных, соответствующих векторам верхних
– векторы
суммарных, взвешенных по вероятности
двойственных переменных, соответствующих векторам верхних 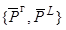 и нижних
и нижних 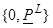 границ изменения
параметров системы (11), (12);
границ изменения
параметров системы (11), (12); 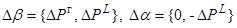 – векторы-столбцы
изменения верхних и нижних
границ параметров системы.
– векторы-столбцы
изменения верхних и нижних
границ параметров системы.
В
большинстве практических случаев для связей выполняется условие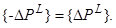 Это приводит к тому,
что изменение показателя надежности
Это приводит к тому,
что изменение показателя надежности 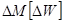 при вариации
параметров системы практически характеризуется только одним вектором
при вариации
параметров системы практически характеризуется только одним вектором 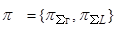 ,
так как второе слагаемое (18) для переменных генерирующей
мощности территориальных зон обращается в ноль, а для пропускных
способностей связей
становится зависящим только от параметра
,
так как второе слагаемое (18) для переменных генерирующей
мощности территориальных зон обращается в ноль, а для пропускных
способностей связей
становится зависящим только от параметра 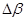 .
Тогда:
.
Тогда:
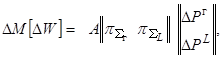 (19)
(19)
где
векторы 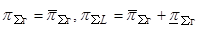 .
.
Выражение
(19) показывает степень влияния переменных
системы на выходной эффект и
позволяет проранжировать и выделить из всего множества переменных
наиболее значимые.
При использовании двойственного симплекс-метода ЛП для оценки
случайного состояния
системы с учетом только балансовых ограничений (9), т.е. без учета
второго
закона Кирхгофа, отпадает необходимость в определении вектора 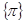 ,
так как двойственная оценка любого столбца симплекс-таблицы
легко определяется (m+1)-й строкой
на
последней итерации простого симплексного алгоритма. Эти двойственные
оценки «работают»
и в условиях неоднозначности прямого решения, так как известно, что при
невырожденном решении (что практически всегда имеет место в наших
задачах),
даже если решение прямой задачи не является однозначным, решение
двойственной
задачи всегда однозначно. Об этом свойстве решений
для пары сопряженных задач доказана
специальная теорема [8].
,
так как двойственная оценка любого столбца симплекс-таблицы
легко определяется (m+1)-й строкой
на
последней итерации простого симплексного алгоритма. Эти двойственные
оценки «работают»
и в условиях неоднозначности прямого решения, так как известно, что при
невырожденном решении (что практически всегда имеет место в наших
задачах),
даже если решение прямой задачи не является однозначным, решение
двойственной
задачи всегда однозначно. Об этом свойстве решений
для пары сопряженных задач доказана
специальная теорема [8].
Остановимся
более подробно на вероятностной
трактовке двойственных переменных линейных моделей. Из выражения (18)
видно,
что двойственные переменные представляют собой не что иное, как сумму
взвешенных по вероятности двойственных оценок для всех расчетных
состояний ЭЭС.
Согласно теории двойственности линейного программирования [8], по
величине
двойственных оценок, полученных на последней итерации симплексного
алгоритма
для переменных, не вошедших в базис, можно судить о степени их влияния
на
выходной эффект системы. Это свойство двойственных оценок дает
возможность
выявить из всего множества переменных те, вариация границ которых
приводит к
наибольшему изменению целевой функции (8). Для k-го
случайного состояния системы (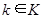 ),
если генерирующая мощность j-й
территориальной зоны с учетом перетоков
взаиморезервирования по связям вышла на свою
верхнюю границу
),
если генерирующая мощность j-й
территориальной зоны с учетом перетоков
взаиморезервирования по связям вышла на свою
верхнюю границу 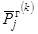 ,
ее двойственная оценка
,
ее двойственная оценка 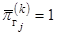 .
Если другие территориальные зоны не
обусловливают дефицита генерирующей мощности, то перетоки мощности по l-м связям ее примыкания к ЭЭС также
выйдут на свои границы (
.
Если другие территориальные зоны не
обусловливают дефицита генерирующей мощности, то перетоки мощности по l-м связям ее примыкания к ЭЭС также
выйдут на свои границы ( или
или 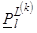 )
и их двойственные оценки примут значения
)
и их двойственные оценки примут значения  или
или 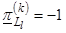 в
зависимости от того, какое направление
перетока мощности по связи принято за положительное.
в
зависимости от того, какое направление
перетока мощности по связи принято за положительное.
Для
многозонной ЭЭС суммарные, взвешенные по вероятности существования
случайных
состояний, двойственные оценки для генерирующих мощностей j-х территориальных зон (j = 1, 2, …, n)
и для пропускных способностей l-х
связей (l = 1, 2, …, m)
адекватны соответствующим интегральным вероятностям дефицита
генерирующей мощности
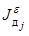 (с учетом перетоков
взаиморезервирования) и перегрузки по пропускной способности связей
(с учетом перетоков
взаиморезервирования) и перегрузки по пропускной способности связей 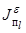 .
Они к тому же равны частным производным от математического
ожидания недоотпуска электроэнергии в объединении ЭЭС по генерирующей мощности
(резерву) j-х территориальных зон и пропускной способности l-х связей
между ними, т.е.
.
Они к тому же равны частным производным от математического
ожидания недоотпуска электроэнергии в объединении ЭЭС по генерирующей мощности
(резерву) j-х территориальных зон и пропускной способности l-х связей
между ними, т.е.
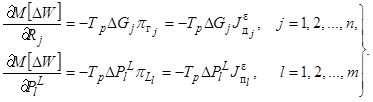 (20)
(20)
Выражения
(19)-(20) позволяют условия оптимальности многозонной ЭЭС (7) для
случая равенства
удельных ущербов в территориальных зонах представить в виде:
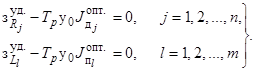 (21)
(21)
В методических
рекомендациях по проектированию развития энергосистем, утвержденных
Минэнерго
России [12] для территориальных
зон ЭЭС предлагается использовать величины нормативных показателей
балансовой
надежности территориальных зон ЭЭС в виде интегральных вероятностей
бездефицитной работы (ρ = 1 – Jд) значением не
менее 0,996. Численное значение и период
действия данного показателя определяется Минэнерго РФ. Этот показатель
соответствует показателю вероятности бездефицитной работы Jд = 0,004.
Выше
было строго показано, что показатель вероятности
бездефицитной работы (Jд) имеет строгое
технико-экономическое
обоснование и связывает между собой два противоречивых понятия (4):
затраты в
обеспечение надежности и компенсационные затраты от ненадежного
электроснабжения. В 70-80-х годах прошлого столетия принимались
следующие величины
показателей, приведенных в расшифровке слагаемых выражения (1).
Удельные замыкающие
затраты в генерирующую мощность (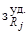 )
принимались равными
22 руб./кВт. Удельный
ущерб (у0)
определялся из отношения
ВВП страны к объему выработанной электрической энергии и принимался
равным
0,6 руб./кВт˚ч. Именно при таких
соотношениях получался обозначенный
выше нормативный показатель Jд = 22/(0,6˚8760) = 0,004
[7, 11].
)
принимались равными
22 руб./кВт. Удельный
ущерб (у0)
определялся из отношения
ВВП страны к объему выработанной электрической энергии и принимался
равным
0,6 руб./кВт˚ч. Именно при таких
соотношениях получался обозначенный
выше нормативный показатель Jд = 22/(0,6˚8760) = 0,004
[7, 11].
В
настоящее время
замыкающие затраты в генерирующую мощность ГТУ-КЭС, по данным ОАО
«Институт
«ЭНЕРГОСЕТЬПРОЕКТ», колеблются в пределах от 28 до
43 тыс.руб./кВт, что
соответствует приведенным к одному году их удельным показателям от 3500
до 5300
руб./кВт. Сегодняшний уровень социально-экономического развития страны
соответствует уровню 80-х годов прошлого столетия –
при централизованном
принципе управления электроэнергетикой бывшего СССР отношение удельного
ущерба
к себестоимости выработки электрической энергии было примерно равным
60÷120,
сегодня это отношение в соответствии с приведенными ниже выкладками
примерно
равно 100÷150. Это говорит о том, что существовавший в СССР
и удовлетворяющий
всех от производителя до потребителя индекс надежности Jд = 0,004
приемлем и сегодня. Это значение
позволяет от обратного найти показатель удельного ущерба
от ненадежности электроснабжения у0.
Он будет определяться соотношением у0 = (3500÷5300)/(8760˚0,004)
≈ 100÷150 руб./кВт˚ч.
Список
литературы:
1. Волков
Э.П.,
Баринов В.А. Методические принципы обоснования развития
электроэнергетики
России в условиях ее либерализации // Изв. АН. Энергетика, 2006. №3.
–С. 3-19.
2. Дьяков
А.Ф. Проблемы надежности и
безопасности энергоснабжения в условиях либерализации и дерегулирования
в
электроэнергетике // Энергетик, 2005. –
№ 8. –
С. 2–9.
3. Дьяков
А.Ф. Проблемы надежности и безопасности больших систем
энергетики // Вести
в электроэнергетике, 2006, –
№2. – C.
3-14.
4. Воропай
Н.И., Иванова Е.Ю., Труфанов В.В., Шевелева Г.И. Принципы и механизмы
обеспечения развития электроэнергетики // Вести в
электроэнергетике,
2006, – №2. – C.
14-21.
5. Воропай
Н.И. Обеспечение надежности электроснабжения потребителей в рыночных
условиях // Методические вопросы исследования
надежности больших
систем энергетики. Вып.57. – Киев: Знания Украины, 2007.
– С. 51-57.
6. Воропай
Н.И. Проблемы исследования и обеспечения надежности либерализованных
систем
энергетики // Надежность систем энергетики:
Методические и практические
задачи. – Новосибирск: Наука, 2005. – С. 6-20.
7. Маркович И.М. Режимы
энергетических систем. – М.:
Энергия, 1969. –351 с.
8. Юдин
Д.Б.,
Гольштейн Е.Г. Линейное
программирование. – М.: Мир,
1966. –276 с.
9. Фокин
Ю.А., Туфанов
В.А. Оценка надежности систем электроснабжения. – М.:
Энергоиздат, 1981. – 224
с.
10. Чукреев
Ю.Я., Чукреев М.Ю. Обеспечение надежности при управлении развитием
электроэнергетических систем для условий реформирования
электроэнергетики. // Известия
РАН. Энергетика, 2008. –№ 4. – С. 39-48.
11. Чукреев
Ю.Я.
Модели обеспечения надежности электроэнергетических систем. –
Сыктывкар: Коми НЦ УрО РАН, 1995. –176 с.
12. Методические
рекомендации по
проектированию развития энергосистем. Утверждены приказом Минэнерго
России №
281 от 30.06.2003.
Literature:
1. Volkov E.P., Barinov
V.A. Principles and reasons of Russian power industry evaluation during
liberalization // AS News. Energy, 2006. #3. -pp.
3-19.(in Russian).
2. Dyiakov A.F. Reliability
and power security issues in conditions of liberalization and
deregulation of
power industry // Power engineer, 2005. – # 8. –
pp. 2–9. (in Russian)
3. Dyiakov A.F. Reliability
and power security issues for large-scale power systems
// News in power
industry, 2006, –
#2. – pp. 3-14. (in
Russian)
4. Voropai N.I., Ivanova
E.Y., Trufanov V.V., Scheveleva G.I. Principles and arrangements of power industry evolution
// News in power
industry, 2006, – #2. – pp. 14-21. (in Russian)
5. Voropai N.I. Reliability
of power supply for customers in economical situation
// Methodical issues
and research of large-scale power systems. Issue.57. – Kiev:
Ukraine knowledge,
2007. – pp. 51-57. (in Russian)
6. Voropai N.I. Research
and reliability issues for liberalized power
systems// Reliability of power
systems: Methodical and practical issues. – Novosibirsk:
Science, 2005. – pp.
6-20. (in Russian)
7. Marcovich I.M. Power systems states.
– M.: Energy, 1969. –351 p. (in
Russian)
8. Judin
D.B., Golshtein E.G. Linear
programming. – M.: Mir,
1966. –276 p. (in Russian)
9.
Fokin Y.A., Tufanov V.A. Power systems reliability assessment.
– M.: Energoizdat,
1981. – 224 p. (in Russian)
10. Chukreyev Y.J., Chukreyev
M.Y. Control of evolution and reliability of power systems in
conditions of
conversional power industry. // RAN News. Energy,
2008. –# 4. – pp.
39-48. (in Russian)
11. Chukreyev
Y.J. Reliability models of power systems. – Syktyvkar: Komi SC UB RAS,
1995. –p 176. (in Russian)