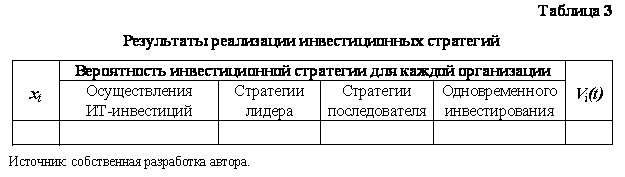|
|
МОДЕЛЬ ОПЦИОННЫХ ИГР ДЛЯ ПРИНЯТИЯ ИНВЕСТИЦИОННЫХ РЕШЕНИЙ В СФЕРЕ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ
Мазоль О.И.
В данной статье анализируются оптимальные инвестиционные решения однородных организаций в условиях конкурентной неопределенной среды. Построена модель опционных игр, которая исследует поведение инвестора в реальном секторе экономики с учетом факторов риска и неопределенности. Разработанная модель дает возможность оптимизировать инвестиционную стратегию организации в сфере информационных технологий в условиях олигополистической конкуренции посредством обоснованного выбора определенного варианта стратегии. Получено оптимальное правило выбора момента инвестирования
In this article is analyzed the optimal investment decisions of homogeneous organizations in a competitive uncertain environment. The model of option games is built, it examines investor behavior in the real economy, taking into account the risks and uncertainties. The developed model makes it possible to optimize the investment strategy of the organization by informed choice of certain variants of options strategies in the field of information technologies under conditions of oligopolistic competition. The optimal rule for choosing the time of investment was obtained
Ключевые слова: ИТ-инвестиции, ИТ-проект, конкуренция, модель, опционные игры, стратегия, теория реальных опционов
Key words: IT-investment, IT-project, Competition, model, option games, strategy, theory of real options
В современных исследованиях недостаточно внимания уделено оценке механизма
воздействия факторов рыночной среды и конкурентной борьбы на эффективность
инвестиций организации в информационные технологии. При принятии решений
инвестор сталкивается со стохастической неопределенностью, которая предполагает
различные вероятные состояния рыночной среды, оказывающие влияние на
эффективность инвестиционных решений. Инвестор имеет дело с существованием
множественных оценок ИТ-эффектов и ИТ-затрат, так как в зависимости от момента
времени реализации инвестиционного решения меняется состояние факторов рыночной
среды, что оказывает влияние на эффективность ИТ-инвестиций. Особенностью
инвестиционных проектов в области информационных технологий является небольшая
продолжительность инвестиционной фазы ИТ-проекта, в связи с чем обоснование
эффективных инвестиционных решений по проектам данного типа требует четкого
выбора момента времени инвестирования.
Предлагаемая
экономико-математическая стохастическая модель опционных игр основана на
применении теорий игр и реальных опционов и позволяет организации оптимизировать
инвестиционную стратегию в условиях олигополистической конкуренции. Организации,
рассматриваемые в качестве игроков, являются однородными, что в свою очередь,
предполагает реализацию ими симметричных стратегий. Предполагается, что
организации уже функционируют на рынке, производят продукцию, а также способны
реализовать инвестиционный проект в будущем, моделируемый как бесконечный
колл-опцион. Данная модель также предполагает существование отрицательных
экстерналий, т.е. реализация одной из организаций инвестиционного проекта
снижает поток доходов другой организации.
Рассматриваемая модель
позволяет организации определить оптимальную стратегию реализации ИТ-инвестиций
относительно аналогичной стратегии конкурента, а также учесть следующие факторы:
- Во-первых, фактор
неопределенности, связанный со случайными колебаниями спроса на планируемый
выпуск продукции и инвестированные ресурсы, необходимые для внедрения ИТ-проекта
(учет данного фактора приводит к необходимости моделировать потоки денежных
средств, связанные с реализацией ИТ‑инвестиций, как случайные процессы).
- Во-вторых, в отличие
от инвестиций в ценные бумаги, предполагается, что ИТ-инвестиции являются
необратимыми, т.е. после внедрения ИТ-проекта их нельзя использовать на другие
цели.
- В-третьих,
учитывается короткий жизненный цикл ИТ-инвестиций. Согласно закону Гордона Мура,
существующая технологическая база ИТ полностью обновляется каждые три года [1,
2].
- В-четвертых, в
предлагаемой модели учитывается фактор инновационности ИТ-проекта. Выбор
технологии является необратимым процессом, а инновационный процесс не зависит от
действий организаций. Поскольку рынок в поиске равновесия стремится к насыщению,
а с течением времени появляются все более совершенные технологии, необратимые
инвестиционные затраты для каждой технологии снижаются с течением времени.
Предлагаемая в данном
параграфе модель принятия инвестиционных решений в условиях конкуренции
основывается на модели Диксита-Пиндика [3, с. 136].
В ней было изучено поведение инвестора, приведенная прибыль которого после
осуществленных инвестиций в некоторый проект описывается случайным процессом
(обычно геометрическим броуновским движением), а инвестиции считаются
невозвратными. Предложенная общая постановка в частных случаях
соответствует дуополии Курно и Штакельберга.
Пусть рыночные условия
соответствуют олигополии, а поведение инвестирующей организации предполагается
рациональным в том смысле, что, наблюдая колебания рыночного спроса, она либо
принимает решение об инвестировании в ИТ-проект (предполагается, что организация
стремится внедрить наиболее современные технологии), либо откладывает принятие
этого решения до наступления более благоприятной ситуации. Предположим, что
организации, действующие на рынке, конкурируют в условиях неопределенности
спроса и олигополистической конкуренции, стремятся максимизировать прибыль,
производят однородную продукцию и являются идентичными (следовательно, реализуют
симметричные стратегии). Обозначим одну организацию через
i,
другую через j,
где
![]() и
i≠j.
Каждая из них имеет возможность осуществить ИТ-инвестиции с необратимыми
издержками Ih>0,
где
и
i≠j.
Каждая из них имеет возможность осуществить ИТ-инвестиции с необратимыми
издержками Ih>0,
где ![]() ,
I1>I2,
что соответствует второму и четвертому предположению данной модели
(инвестиционные затраты на ИТ-проект являются необратимыми, а инновационный
процесс снижает стоимость информационных технологий). Пусть
r
– ставка дисконтирования (r>0),
φ – коэффициент,
учитывающий моральный износ информационных технологий (согласно закону Гордона
Мура, существующая технологическая база ИТ полностью обновляется каждые три
года), что соответствует третьему предположению данной модели (ИТ-инвестиции
обладают коротким жизненным циклом). Модифицированная ставка дисконтирования
rm
для информационных технологий рассчитывается следующим образом:
,
I1>I2,
что соответствует второму и четвертому предположению данной модели
(инвестиционные затраты на ИТ-проект являются необратимыми, а инновационный
процесс снижает стоимость информационных технологий). Пусть
r
– ставка дисконтирования (r>0),
φ – коэффициент,
учитывающий моральный износ информационных технологий (согласно закону Гордона
Мура, существующая технологическая база ИТ полностью обновляется каждые три
года), что соответствует третьему предположению данной модели (ИТ-инвестиции
обладают коротким жизненным циклом). Модифицированная ставка дисконтирования
rm
для информационных технологий рассчитывается следующим образом:
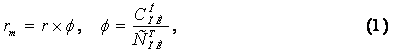
где
![]() –
нормативный срок полезного использования информационных технологий (согласно
классификатору основных средств),
–
нормативный срок полезного использования информационных технологий (согласно
классификатору основных средств),
![]() =
6 лет;
=
6 лет;
![]() –
срок полезного использования информационных технологий (согласно закону Гордона
Мура)
–
срок полезного использования информационных технологий (согласно закону Гордона
Мура) ![]() =
3 года.
=
3 года.
Неопределенность потока денежных средств, формируемых ИТ‑инвестициями,
описывается геометрическим броуновским движением (первое предположение данной
модели):
![]()
![]()
где
a
– тенденция, определяет ежегодный темп
роста потока денежных средств, формируемых ИТ-инвестициями,
a<r,
%;
σ
– волатильность, определяет ежегодное
среднеквадратичное отклонение потока денежных средств от ИТ-инвестиций, %;
dt
– приращение времени;
dwt
– приращение винеровского
случайного процесса.
Поток доходов, который
способна получить организация в определенный период времени от ИТ-инвестиций,
равен:
![]()
где для
![]()
![]() (5)
(5)
где xt – стохастический шок спроса, следующий процессу геометрического броуновского движения и описывающий динамику потока денежных средств от ИТ‑инвестиций, ден. ед.;
![]() –
детерминистический параметр спроса, описывающий вклад в функцию потока доходов.
–
детерминистический параметр спроса, описывающий вклад в функцию потока доходов.
Параметр
![]() может
принимать следующие значения:
может
принимать следующие значения:
D00 – означает, что обе организации еще не реализовали ИТ-проект (однако поток доходов, равный xt∙D00, существует, поскольку организации являются действующими на рынке);
D10 – означает, что организация i осуществила ИТ-проект, т.е. реализует стратегию лидера, а организация j – нет, а значит, реализует стратегию последователя;
D01 – означает, что организация i реализует стратегию последователя, а организация j – стратегию лидера;
D11 – означает, что обе организации одновременно осуществили ИТ‑инвестиции, т.е. реализуют стратегию совместных инвестиций.
Различные значения параметра
![]() определяют
соответствующие уровни потока доходов для каждой организации. Например, поток
доходов, равный xt∙D10,
выше потока доходов, равного xt ∙D01,
т.е. стратегии лидера соответствует более высокий уровень потока доходов, чем
стратегии последователя. Кроме того, поскольку рассматривается модель с
симметричными стратегиями, если одна организация получает поток доходов, равный
xt∙D10,
то вторая организация получает поток доходов, равный xt∙D01,
и т.д.
определяют
соответствующие уровни потока доходов для каждой организации. Например, поток
доходов, равный xt∙D10,
выше потока доходов, равного xt ∙D01,
т.е. стратегии лидера соответствует более высокий уровень потока доходов, чем
стратегии последователя. Кроме того, поскольку рассматривается модель с
симметричными стратегиями, если одна организация получает поток доходов, равный
xt∙D10,
то вторая организация получает поток доходов, равный xt∙D01,
и т.д.
Существование между организациями отрицательных экстерналий
налагает на параметр
![]() дополнительное
ограничение, выражаемое следующим неравенством:
дополнительное
ограничение, выражаемое следующим неравенством:
![]()
Преимущество стратегии лидера перед другими стратегиями можно выразить следующим неравенством:
![]()
Неравенство (7) показывает, что уровень потока доходов для стратегии лидера выше, чем стратегии последователя (для одной и той же величины потока доходов xt и тех же инвестиционных затрат I).
До осуществления инвестиций, т.е. исполнения опциона инвестирования, когда ожидаемый поток доходов от инвестиций меньше инвестиционного порога для организации-лидера (такого ожидаемого потока доходов от инвестиций, при котором организация-лидер осуществит проект), ожидаемый поток доходов для обеих организаций, V(xt), равен сумме текущего бесконечного потока доходов и опциона на осуществление инвестиций за вычетом потерь от конкуренции, вызванных влиянием отрицательных экстерналий инвестиций организации-последователя:
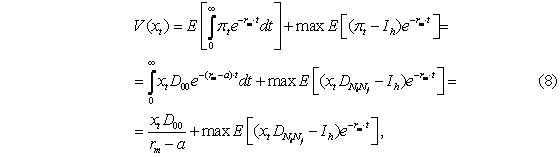
где E(∙) – математическое ожидание.
Существует три возможности относительно времени инвестирования двумя конкурирующими организациями. Во-первых, организация i может инвестировать первой и стать лидером. Напротив, организация j может инвестировать раньше организации i, и тогда организация i станет последователем. Наконец, организации могут инвестировать одновременно. Вычислим поток доходов от ИТ-инвестиций организаций, соответствующий упомянутым выше трем ситуациям. Следуя стандартному подходу динамического программирования, проанализируем задачу методом обратной индукции во времени. Сначала выведем оптимальную стратегию организации-последователя, предполагая, что организация-лидер уже осуществила инвестиции. Далее проанализируем оптимальное решение организации-лидера, предполагая, что организация-лидер знает следующее: организация-последователь осуществит в будущем свою оптимальную стратегию. При этом каждая из организаций может быть лидером. В последнюю очередь исследуем случай совместного инвестирования.
Рассмотрим инвестиционное решение последователя
(организации i) в момент
t, где t – момент инвестирования
лидера (организации j). Организация
j предпримет инвестирование, если поток денежных
средств от ИТ-инвестиций достаточно высок, т.е. если случайный процесс
xt превзойдет некоторое пороговое
значение, обозначаемое
![]() .
При xt, поток доходов от
ИТ‑инвестиций организации i как последователя,
.
При xt, поток доходов от
ИТ‑инвестиций организации i как последователя,
![]() ,
определяется следующим образом:
,
определяется следующим образом:
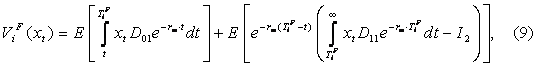
где
![]()
где
![]() –
момент инвестирования организации i как
последователя, лет.
–
момент инвестирования организации i как
последователя, лет.
Первый интеграл в выражении (9) соответствует текущему значению потока доходов от ИТ-инвестиций, получаемого до осуществления инвестирования. Вторая составляющая (9) описывает текущее значение потока доходов, полученного после осуществления инвестирования.
Таким образом, представленная выше постановка задачи соответствует задаче об оптимальной остановке в непрерывном времени. Следуя стандартному подходу динамического программирования (используя принцип оптимальности Беллмана[1] [4, с. 105] и фундаментальное уравнение оптимальности Беллмана [4, с. 228, 340]), получим следующее уравнение Беллмана для данной задачи:
![]()
Уравнение (11) показывает, что для нейтральной к риску организации ожидаемый уровень изменения стоимости инвестиционной возможности в течение интервала времени, dt, равен уровню безрисковой доходности, т.е. ожидаемой норме прироста капитала.
Используя лемма Ито для расчета dVF(xt) и уравнение (2) для расчета dxt, получим:
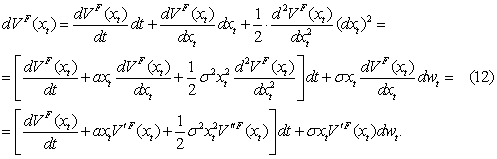
Согласно лемма Ито,
![]() ,
следовательно, уравнение (12) примет вид:
,
следовательно, уравнение (12) примет вид:
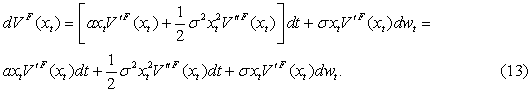
Согласно лемма Ито, E(dwt)=0, следовательно, получим:
![]()
Отсюда уравнение (12) примет вид:
![]()
Разделив уравнение (15-2.36) на dt, получим:
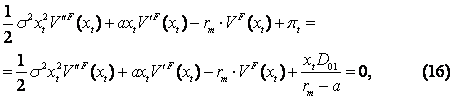
где
![]()
Три первых элемента уравнения (16) соответствуют однородной компоненте обыкновенного дифференциального уравнения второго порядка, а последний элемент – неоднородная компонента, представляющая собой поток доходов организации-последователя до осуществления ею ИТ-инвестиций, когда организация-лидер уже осуществила инвестирование.
Для решения уравнения (16) относительно
![]() необходимо,
чтобы
необходимо,
чтобы
![]() удовлетворяло
следующим условиям [3, с. 141]:
удовлетворяло
следующим условиям [3, с. 141]:
![]()
![]()
![]()
где
![]() –
оптимальный инвестиционный порог организации последователя, ден. ед.
–
оптимальный инвестиционный порог организации последователя, ден. ед.
Условие (18) показывает, что если организация инвестирует,
то она получает поток доходов, равный
![]() .
.
Чтобы удовлетворять условию (19), общее решение уравнения (16) будет следующим:
![]()
где A, B – константы решения обыкновенного дифференциального уравнения второго порядка;
β1, β2 – положительный и
отрицательный корни квадратного уравнения
![]() ,
,
![]() .
.
Первые два элемента в уравнении (20) представляют собой однородное решение обыкновенного дифференциального уравнения второго порядка, а третий элемент является частным решением, отражающим поток доходов организации-последователя до осуществления ею ИТ-инвестиций.
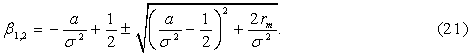
Согласно ограничению (17), B=0 (β2 – отрицательный корень), поскольку в соответствии с экономической логикой если xt стремится к нулю, то и ожидаемый поток доходов от ИТ-инвестиций также стремится к нулю. Следовательно, общее решение (20) уравнения (16) примет вид:
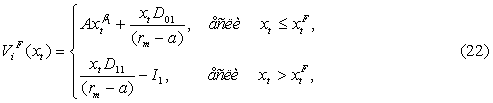
где ![]() –
поток доходов организации i как последователя в
момент времени t, ден. ед.;
–
поток доходов организации i как последователя в
момент времени t, ден. ед.;
![]() –
оптимальный инвестиционный порог организации последователя, ден. ед.
–
оптимальный инвестиционный порог организации последователя, ден. ед.
Выражение (22) интерпретируется следующим образом: первая
строка представляет собой текущее значение потока доходов, формируемого
ИТ‑инвестициями, в том случае, если последователь не инвестирует немедленно.
Первое слагаемое является потоком доходов, формируемым ИТ‑инвестициями, а второе
слагаемое представляет собой поток доходов организации-последователя до
осуществления ею ИТ-инвестиций. Вторая строка соответствует текущему значению
потока доходов, вызванного немедленным инвестированием, что соответствует
экономической сущности ограничения (18)[2].
Для полного решения
системы уравнений (22) необходимо найти две неизвестные величины: константу А
и инвестиционный порог ![]() .
.
После решения уравнения (16), для
инвестиционного порога
![]() ограничения
(18) и (19) примут следующий вид:
ограничения
(18) и (19) примут следующий вид:
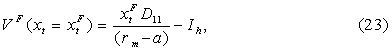
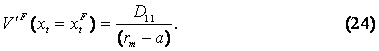
Пусть
![]() ,
тогда, подставив уравнение (23) и уравнение (24) в первую строку системы
уравнений (22), получим:
,
тогда, подставив уравнение (23) и уравнение (24) в первую строку системы
уравнений (22), получим:
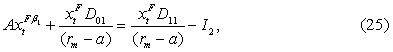
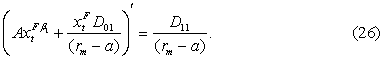
Откуда после
соответствующих перестановок получим:

![]()
Подставив константу
А в систему уравнений (22), получим:
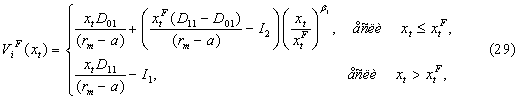
Следуя представленным выше результатам, можно определить поток доходов организации i, если она инвестирует первой, т.е. станет лидером. Следовательно, поток доходов организации i при xt, где t – момент инвестирования, равен:
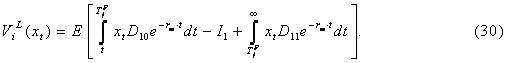
Первый интеграл в выражении (30) соответствует текущему значению потока доходов лидера, получаемого до того, как последователь осуществит аналогичные ИТ-инвестиции за вычетом необратимых инвестиционных затрат. Вторая составляющая (30) описывает текущее значение потока доходов лидера, полученного после осуществления инвестирования последователем. Таким образом, выбрав стратегию лидера, организация i сначала проходит монопольную стадию с потоком доходов, равным xtD10, а затем, когда организация последователь j также осуществит ИТ-инвестиции в период времени t=TF, поток доходов снизится до величины xtD11.
Используя результаты решения задачи для организации-последователя, можно выразить поток доходов от ИТ‑инвестиций для организации i в момент времени t. Поток доходов организации-лидера в течение монопольной стадии можно выразить следующим образом:
![]()
При этом поток доходов в течение монопольной стадии
![]() организация
i как лидер получит, если в период времени
t=TF
выполняется условие
организация
i как лидер получит, если в период времени
t=TF
выполняется условие ![]() .
.
Таким образом, используя аналогичный подход, что и для
расчета потока доходов организации-последователя, поток доходов для
организации-лидера в течение монопольной стадии
![]() можно
выразить следующим дифференциальным уравнением:
можно
выразить следующим дифференциальным уравнением:
![]()
где ![]()
Три первых элемента уравнения (32) соответствуют однородной компоненте обыкновенного дифференциального уравнения второго порядка, а последний элемент – неоднородная компонента, представляющая собой поток доходов организации-лидера от ИТ-инвестиций до того, как организация-последователь осуществит ИТ-инвестиции. Аналогично, как и для организации-последователя, общее решение дифференциального уравнения (32) состоит из двух частей: во-первых, однородного решения обыкновенного дифференциального уравнения второго порядка, а во-вторых, частного решения, отражающего поток доходов организации-лидера до осуществления организацией-последователем ИТ‑инвестиций:
![]()
где B – константа решения
обыкновенного дифференциального уравнения второго порядка,
B<0;
β1 – положительный корень квадратного
уравнения ![]() ,
,
![]() .
.
Согласно уравнению (31), поток доходов организации i как лидера можно определить следующим образом:
![]()
Следовательно, общее решение (33) уравнения (32) примет вид:
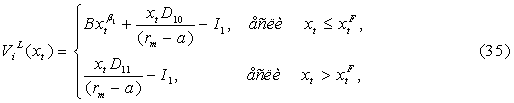
где ![]() –
поток доходов организации i как лидера в момент
времени t, ден. ед.;
–
поток доходов организации i как лидера в момент
времени t, ден. ед.;
![]() –
оптимальный инвестиционный порог организации последователя, ден. ед.
–
оптимальный инвестиционный порог организации последователя, ден. ед.
Для полного решения
системы уравнений (35) необходимо найти константу
B. Главная разница
между константой B и константой
A из системы уравнений (22) заключается в том, что
константа B является отрицательной, отражая
факт потерь, связанных с возможностью в будущем исполнения инвестиций
последователем. Соответствующее ограничение, которому должно удовлетворять
уравнение (32) в точке входа последователя (![]() ):
):

Уравнение (36) показывает, что в точке
![]() в
течение монополистической стадии поток доходов лидера равен потоку доходов
одновременного инвестирования. Приравняв уравнение (33) и уравнение (36),
получим значение константы B:
в
течение монополистической стадии поток доходов лидера равен потоку доходов
одновременного инвестирования. Приравняв уравнение (33) и уравнение (36),
получим значение константы B:
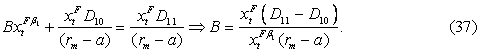
Значение константы B является отрицательным, поскольку D11<D10. Это означает, что эффектом инвестирования последователя является снижение потока доходов лидера, что соответствует экономической логике в данной олигополии.
Подставив константу
B
в уравнение (33), получим поток
доходов лидера, ![]() ,
в течение монопольной стадии:
,
в течение монопольной стадии:
![]()
Определив поток
доходов лидера в течение монопольной стадии, можно вычислить общий поток доходов
лидера, ![]() :
:

Первая строка выражения (39) представляет собой чистое
современное значение потока доходов лидера, формируемого ИТ-инвестициями, до
того, как последователь осуществил инвестирование за вычетом текущего значения
потери будущих доходов вследствие инвестиций последователя. Вторая строка
соответствует чистому текущему значению потока доходов в ситуации, когда для
лидера оптимальным решением является немедленное инвестирование.
Возможно, что организации решат инвестировать одновременно. Используя результаты решения задачи для организации-последователя, поток доходов организации i, инвестирующей при оптимальном инвестиционном пороге одновременно с организацией j, для t≤TS можно определить следующим образом:
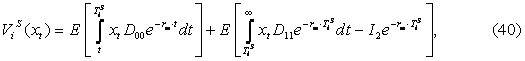
где
![]()
где ![]() –
оптимальный инвестиционный порог одновременного инвестирования.
–
оптимальный инвестиционный порог одновременного инвестирования.
Первый интеграл в выражении (40) соответствует текущему
значению потока доходов, получаемого организациями до осуществления
ИТ‑инвестиций. Вторая составляющая соответствует текущему значению потока
доходов, вызванных одновременным инвестированием. Инвестиционный порог
![]() существует,
пока D11 больше, чем
D00. В противном случае оптимальным для
организаций является воздержаться от инвестирования.
существует,
пока D11 больше, чем
D00. В противном случае оптимальным для
организаций является воздержаться от инвестирования.
Таким образом, используя аналогичный подход, что и для
расчета потока доходов организации-последователя и организации-лидера, поток
доходов для организации, выполняющей стратегию одновременного инвестирования
![]() ,
можно выразить следующим дифференциальным уравнением:
,
можно выразить следующим дифференциальным уравнением:
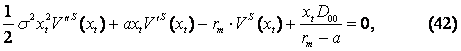
где ![]()
Три первых элемента уравнения (42) соответствуют однородной компоненте обыкновенного дифференциального уравнения второго порядка, а последний элемент – неоднородная компонента, представляющая собой поток доходов для обеих организаций до того, как какая-либо из них осуществит ИТ‑инвестиции. Аналогично, как и для организации-последователя, общее решение дифференциального уравнения (42) состоит из двух частей: во-первых, однородного решения обыкновенного дифференциального уравнения второго порядка, а во-вторых, частного решения, отражающего поток доходов организации до осуществления ИТ‑инвестиций:
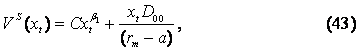
где С – константа решения обыкновенного дифференциального уравнения второго порядка;
β1 – положительный корень квадратного
уравнения ![]() ,
,
![]() .
.
Следовательно, общее решение (43) уравнения (42) примет вид:
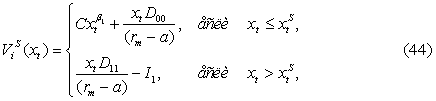
где ![]() –
поток доходов организации i, осуществляющей в
момент времени t стратегию одновременного
инвестирования, ден. ед.;
–
поток доходов организации i, осуществляющей в
момент времени t стратегию одновременного
инвестирования, ден. ед.;
![]() –
оптимальный инвестиционный порог одновременного инвестирования для обеих
организаций, ден. ед.
–
оптимальный инвестиционный порог одновременного инвестирования для обеих
организаций, ден. ед.
Выражение (44) интерпретируется следующим образом: первая
строка представляет собой текущее значение потока доходов, формируемого
ИТ‑инвестициями, в том случае, если организации не инвестируют немедленно, а
инвестируют одновременно с течением времени, когда
![]() превысит
превысит
![]() .
Первое слагаемое является потоком доходов, формируемым ИТ‑инвестициями, а второе
слагаемое представляет собой поток доходов организации до осуществления ею
ИТ-инвестиций. Вторая строка соответствует текущему значению потока доходов,
вызванных немедленным инвестированием, что соответствует экономической сущности
ограничения (18).
.
Первое слагаемое является потоком доходов, формируемым ИТ‑инвестициями, а второе
слагаемое представляет собой поток доходов организации до осуществления ею
ИТ-инвестиций. Вторая строка соответствует текущему значению потока доходов,
вызванных немедленным инвестированием, что соответствует экономической сущности
ограничения (18).
Для полного решения
системы уравнений (44), необходимо найти две неизвестные величины: константу
C
и инвестиционный порог одновременного инвестирования
![]() .
.
После решения уравнения (42) для
инвестиционного порога
![]() ограничения
(18) и (19) примут следующий вид:
ограничения
(18) и (19) примут следующий вид:

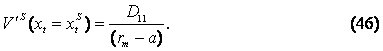
Пусть
![]() ,
тогда, подставив уравнение (45) и уравнение (46) в первую строку системы
уравнений (44), получим:
,
тогда, подставив уравнение (45) и уравнение (46) в первую строку системы
уравнений (44), получим:
![]()
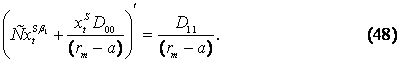
Откуда после
соответствующих перестановок, получим:

![]()
Подставив константу А в систему уравнений (44), получим поток доходов организации i при одновременном осуществлении ИТ-инвестиций:

Выражение (51) интерпретируется следующим образом: первая
строка представляет собой текущее значение потока доходов, формируемого
ИТ‑инвестициями, в том случае, если организации не инвестируют немедленно, а
инвестируют одновременно с течением времени, когда
![]() превысит
превысит
![]() .
Первое слагаемое представляет собой поток доходов организации до осуществления
ею ИТ-инвестиций, а второе слагаемое является потоком доходов, формируемым
ИТ‑инвестициями. Вторая строка в выражении (51) соответствует потоку доходов
организации i, если одновременное
инвестирование осуществляется немедленно.
.
Первое слагаемое представляет собой поток доходов организации до осуществления
ею ИТ-инвестиций, а второе слагаемое является потоком доходов, формируемым
ИТ‑инвестициями. Вторая строка в выражении (51) соответствует потоку доходов
организации i, если одновременное
инвестирование осуществляется немедленно.
Согласно Д. Тжиссену
[5], вероятность того, что организация i
осуществит ИТ‑инвестиции (![]() )
в период времени t
при условии исполнения
симметричных стратегий, можно определить следующим образом:
)
в период времени t
при условии исполнения
симметричных стратегий, можно определить следующим образом:
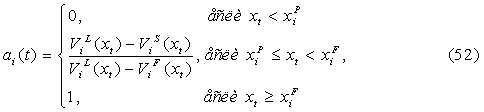
где
![]() >
>![]() ,
,
![]()
![]()
где![]() –
инвестиционный порог, при котором оптимальная стратегия лидера соответствует
стратегии последователя.
–
инвестиционный порог, при котором оптимальная стратегия лидера соответствует
стратегии последователя.
Вероятность того, что обе организации осуществят
ИТ-инвестиции одновременно (![]() )
в период времени t, равна:
)
в период времени t, равна:
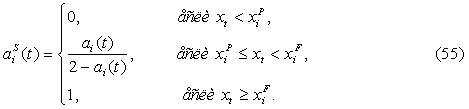
Поскольку, организации осуществляют симметричные стратегии
то, соответственно, вероятности того, что они будут реализовывать как стратегию
лидера (![]() ),
так и последователя (
),
так и последователя (![]() )
в период времени t, равны и могут быть
определены следующим образом:
)
в период времени t, равны и могут быть
определены следующим образом:
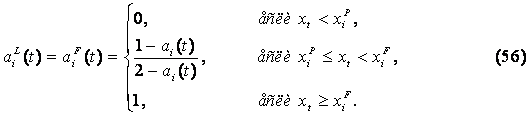
;
В результате, общий вероятностный текущий поток доходов от ИТ‑инвестиций организации i в период времени t можно выразить в виде реализации смешанной стратегии и вычислить по следующей формуле:
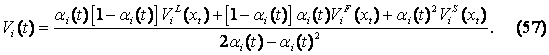
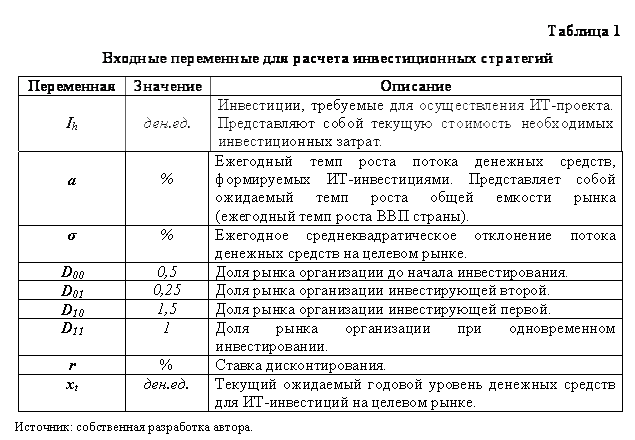
Основываясь на
представленной выше модели, оценку инвестиционной стратегии организации по
реализации ИТ-проекта с учетом влияния конкуренции можно представить в виде
таблиц 1, 2 и 3. Таблица 1 представляет собой набор входных данных, необходимых
для расчета модели. В таблице 2 осуществляется группировка переменных,
рассчитанных с помощью представленной выше модели. Таблица 3 является
аналитической, представляющей в наглядной форме вероятности реализации всех
возможных инвестиционных стратегий, соответствующие им значения потоков доходов,
формируемых ИТ-инвестициями, а также возможный окончательный результат
реализации ИТ-проекта, представляющий собой средневзвешенный ожидаемый поток
доходов для каждой организации.
Таким образом,
разработанная модель опционных игр позволяет оптимизировать инвестиционную
стратегию организации в сфере информационных технологий в условиях
олигополистической конкуренции посредством обоснованного выбора определенного
варианта стратегии. Отличительными особенностями представленной в статье модели
являются: во-первых, исследование поведения и стратегического взаимодействия уже
функционирующих на рынке организаций; во-вторых, учет короткого жизненного цикла
ИТ-инвестиций на основе включения в модель нормированного коэффициента
морального износа информационных технологий; в-третьих, учет
фактора инновационности ИТ-проекта путем
моделирования для конкурирующих организаций различных объемов инвестиционных
затрат. Полученные результаты можно использовать для формирования
рекомендаций по выработке наиболее успешной инвестиционной стратегии в сфере
информационных технологий, позволяющей учесть действия конкурентов. Список литературы: 1.
Jovanovich, B. Moore’s law and learning by doing / B. Jovanovic, P.L.
Rousseau // Review of Economic Dynamics. 2002. № 5. P. 346-375. 2.
Noyce, R.N. Microelectronics / R.N. Noyce //
Scientific American. 1977. Vol. 237, № 3. P. 62-69. 3.
Dixit, A.K. Investment under uncertainty / A.K. Dixit, R.S. Pindyck.
Princeton: Princeton University Press, 1994. 454 p. 4.
Белманн.
Р.
Динамическое программирование
/ Р.
Беллман.
М.:
Изд-во
иностр.
лит.,
1960. 400 с. 5.
Strategic investment uncertainty and information spillovers / J.J.
Thijssen [et al.] // Economic Theory. 2006. №28. P. 399–424. Literature: 1.
Jovanovich, B. Moore’s law and learning by doing / B. Jovanovic, P.L.
Rousseau // Review of Economic Dynamics. 2002. № 5. P. 346-375. 2.
Noyce, R.N. Microelectronics / R.N. Noyce //
Scientific American. 1977. Vol. 237, № 3. P. 62-69. 3.
Dixit, A.K. Investment under uncertainty / A.K. Dixit, R.S. Pindyck.
Princeton: Princeton University Press, 1994. 454 p. 4.
Bellman, R. Dynamic programming
/ R. Bellman.
М.:
Foreign literature
publishing house,
1960. 400 p. 5.
Strategic
investment uncertainty and information spillovers / J.J. Thijssen [et al.] //
Economic Theory. 2006. №28. P. 399–424.
[1] Принцип оптимальности
Беллмана – оптимальное поведение обладает
тем свойством, что каковы бы ни были
первоначальное состояние и решение в начальный
момент, последующее решение должно составлять
оптимальное поведение относительно состояния,
получающегося в результате первого решения.
[2] Если
стохастический шок спроса
xt,
следующий процессу геометрического броуновского
движения и описывающий динамику потока доходов
от ИТ‑инвестиций, окажется выше инвестиционного
порога последователя